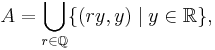Fσ set
In mathematics, an Fσ set (said F-sigma set) is a countable union of closed sets. The notation originated in France with F for fermé (French: closed) and σ for somme (French: sum, union).
In metrizable spaces, every open set is an Fσ set. The complement of an Fσ set is a Gδ set. In a metrizable space, any closed set is a Gδ set.
The union of countably many Fσ sets is an Fσ set, and the intersection of finitely many Fσ sets is an Fσ set.
Examples
Each closed set is an Fσ set.
The set 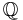 of rationals is an Fσ set. The set
of rationals is an Fσ set. The set 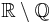 of irrationals is not a Fσ set.
of irrationals is not a Fσ set.
In a Tychonoff space, each enumerable set is an Fσ set, because a point 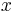 is closed.
is closed.
For example, the set  of all points
of all points 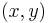 in the Cartesian plane such that
in the Cartesian plane such that 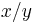 is rational is an Fσ set because it can be expressed as the union of all the lines passing through the origin with rational slope:
is rational is an Fσ set because it can be expressed as the union of all the lines passing through the origin with rational slope:
where 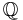 , is the set of rational numbers, which is a countable set.
, is the set of rational numbers, which is a countable set.
See also
- Gδ set — the dual notion.
- Borel hierarchy